
Hvad bestemmer nøjagtighed - et af et våbens hovedkarakteristika? Naturligvis fra kvaliteten af tønde og patron. Lad os udsætte patronen for nu, men overvej processens fysik.
Tag en metalstang eller et rør lavet af elastisk metal og fastgør det stift i en massiv bund. Så vi får en model af enheden under undersøgelse. Nu, hvis vi rammer stangen, er det ligegyldigt på hvilket sted og i hvilken retning, enten trække den tilbage eller klemme den, eller endelig sætte en patron i røret og affyre et skud, vil vi se, at stangen (tønde) er kommet i en dæmpet oscillerende bevægelse. Disse vibrationer nedbrydes til det enkleste, og hver type af en så simpel vibration af tønden vil påvirke nøjagtigheden (nøjagtigheden) af skydning på sin egen måde.
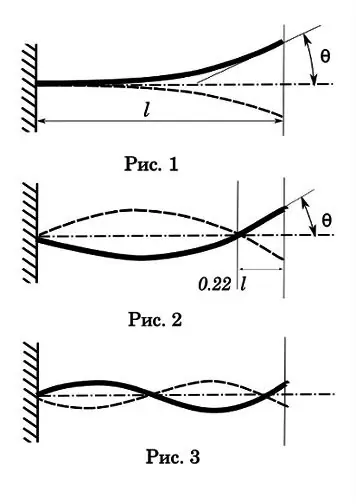
Lad os starte med første orden eller pitch vibrationer. Som du kan se (fig. 1), har en sådan svingning kun en knude ved fastgørelsespunktet, den største amplitude, den længste henfaldstid og den længste svingningstid i en periode. Denne gang er 0,017-0,033 sek. Kuglens rejsetid gennem boringen er 0, 001-0, 002 sek. Det vil sige betydeligt mindre end cyklussen for en oscillation, hvilket betyder, at denne type oscillation ikke har en signifikant effekt på nøjagtigheden af et enkelt skud. Men med automatisk optagelse kan et interessant billede vise sig. Lad os sige, at brandhastigheden er 1200 rds / min, dvs. tid af en cyklus - 0,05 sek. Med en førsteordens oscillationsperiode på 0, 025 sek har vi et multipelt frekvensforhold. Og dette er en uundværlig betingelse for resonans med alle de efterfølgende konsekvenser - våbnet begynder at ryste med en sådan kraft, at det kan falde fra hinanden.
Lad os gå videre til svingninger af anden orden (fig. 2). Men jeg foreslår, at humanistiske studerende først foretager et eksperiment for at fjerne manglerne i uddannelse inden for fysik. Du skal tage en lille dreng (du kan en pige), sætte ham på en gynge og svinge. Før du er et pendul. Stå ved siden af gyngen, og prøv at slå drengen med bolden. Efter en række forsøg kommer du til den konklusion, at den bedste måde at ramme er, når målet er i den første oscillationsfase - den maksimale afvigelse fra ligevægtspunktet. På dette tidspunkt har målet nul hastighed.
Lad os se på andenordens diagram. Den anden vibrationsknude er placeret cirka 0,22 fra enden af tønderen. Dette punkt er en naturlov, det er umuligt at skabe sådanne vibrationer for udliggerstrålen, så den anden knude falder i den frie ende. Det er, hvor det er og afhænger ikke af tøndeens længde.
Oscillationsamplituden for andenordens ordning er lavere, men oscillationstiden er allerede sammenlignelig med tidspunktet for kuglens passage gennem boringen-0, 0025-0, 005 sek. Så for enkeltskydning er dette allerede af interesse. For at gøre det klart, hvad vi taler om, skal du forestille dig en tønde på 1 meter. Kuglen bevæger sig gennem hele tønden på 0, 001 sekunder. Hvis oscillationsperioden er 0,004 sek., Når kuglen forlader tønden, vil tønden nå sin maksimale bøjning i den første fase. Spørgsmålet til humaniora er - på hvilket tidspunkt (i hvilken fase) er det bedst at skyde en kugle ud af tønden for at sikre konsekvens af resultater? Husk gyngen. Ved nulpunktet er vektoren for bagagerumsafbøjningshastigheden maksimal. Det er sværere for en kugle at ramme dette punkt på tøndeudskæringen, den har også sin egen fejl i hastighed. Det vil sige, at det bedste øjeblik for kuglen at flyve ud vil være, når tønden er på det højeste punkt i den første afbøjningsfase - som i figuren. Derefter kompenseres ubetydelige afvigelser i kuglehastigheden af den længere tid, tønden bruger i sin mest stabile fase.
En grafisk fremstilling af dette fænomen kan tydeligt ses i diagrammet (fig. 4-5). Her - Δt er den tidsfejl, hvormed kuglen krydser tøndemundingen. I fig. 4 er ideel, når den gennemsnitlige bullet-starttid falder sammen med nulfasen af tøndeoscillationen. (Matematikere! Jeg ved, at hastighedsfordelingen er ikke-lineær.) Det skraverede område er banernes spredningsvinkel.
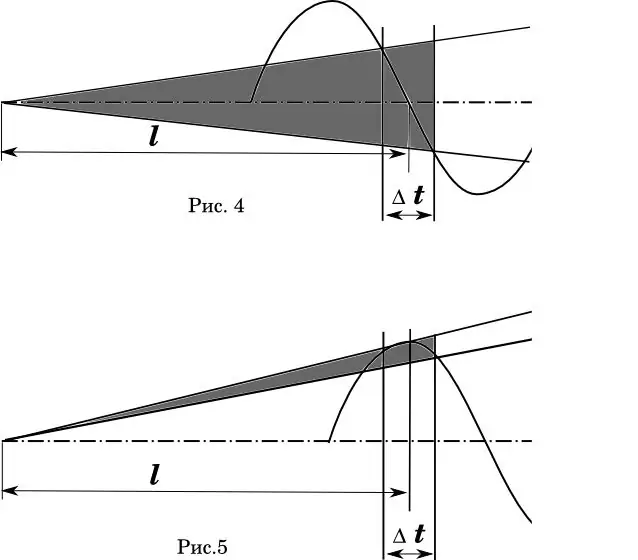
I fig. 5 forbliver cylinderlængden og hastighedsfejlen den samme. Men fasen af tøndebøjningen forskydes, så den gennemsnitlige afgangstid falder sammen med tønderens maksimale afbøjning. Er kommentarer overflødige?
Tja, er det lyset værd? Hvor alvorlige kan afvigelserne forårsaget af andenordens svingninger være? Alvorlig og meget alvorlig. Ifølge den sovjetiske professor Dmitry Aleksandrovich Ventzel blev der i et af eksperimenterne opnået følgende resultater: radius af medianafvigelsen steg med 40% med en ændring i tøndelængden med kun 100 mm. Til sammenligning kan en tøndebehandling af høj kvalitet forbedre nøjagtigheden med kun 20%!
Lad os nu se på formlen for vibrationsfrekvensen:

hvor:
k - koefficient for andenordens svingninger - 4, 7;
L er tønde længde;
E er elasticitetsmodulet;
Jeg er afsnittets inertimoment;
m er stammens masse.
… og gå videre til analysen og konklusionerne.
Den indlysende konklusion fra figur 4-5 er kuglehastighedsfejl. Det afhænger af pulverets kvalitet og dets vægt og densitet i patronen. Hvis denne fejl er mindst en fjerdedel af cyklustiden, kan alt andet opgives. Heldigvis har videnskab og industri opnået meget stor stabilitet i denne sag. Og for de mere sofistikerede (i f.eks. Bænkstøtte) er der alle betingelser for selvsamling af patroner for at justere kuglens frigivelsesfase nøjagtigt til tønde længden.
Så vi har en patron med den lavest mulige hastighedsvariation. Tønderlængden blev beregnet ud fra dens maksimale vægt. Spørgsmålet om stabilitet opstår. Vi ser på formlen. Hvilke variabler påvirker ændringen i svingningsfrekvensen? Tønde længde, elasticitetsmodul og masse. Tønden opvarmes under affyring. Kan varme ændre tønde længde, så nøjagtigheden påvirkes. Ja og nej. Ja, da dette tal ligger inden for hundrededele af en procent for en temperatur på 200 C. Nej, da ændringen i stålets elastiske modul for den samme temperatur er omkring 8-9%, for 600C er det næsten to gange. Det vil sige mange gange højere! Tønden bliver blødere, tøndeens bøjningsfase forskydes fremad i det øjeblik kuglen forlader, falder nøjagtigheden. Hvad siger en tankevækkende analytiker? Han vil sige, at det er umuligt at få maksimal nøjagtighed på en tønde længde i kold og varm tilstand! Våbnet kan have en bedre ydeevne med enten en kold eller varm tønde. Derfor opnås to klasser af våben. Den ene er for bagholdsaktioner, når målet skal rammes fra det første - "kolde" skud, fordi nøjagtigheden af det andet vil være værre på grund af den uundgåelige opvarmning af tønden. I et sådant våben er der ikke noget presserende behov for automatisering. Og den anden klasse er automatiske rifler, hvis tønde er tilpasset den varme tønde. I dette tilfælde kan en mulig miss på grund af den lave nøjagtighed af et koldskud kompenseres for et hurtigt efterfølgende varmt og mere præcist skud.
EF Dragunov kendte fysikken i denne proces meget godt, da han designede sit gevær. Jeg foreslår, at du gør dig bekendt med historien om hans søn Alexei. Men først skal nogen bryde deres hjerner. Som du ved, nærmede to prøver af Konstantinov og Dragunov finalen i konkurrencen om et snigskytteriffel. Designerne var venner og hjalp hinanden i alt. Så Konstantinovs riffel var "indstillet" til kold tilstand, Dragunovs riffel til "varm". I forsøget på at forbedre nøjagtigheden af rivalens riffel affyrer Dragunov sin riffel med lange pauser.

Lad os se på formlen igen. Som du kan se, afhænger frekvensen også af tøndeens masse. Stammens masse er konstant. Men hård kontakt med forenden giver en uforudsigelig positiv feedback til tønden. Systemet-tønde-forend-arm (støtte) vil have et andet inertimoment (et sæt masser i forhold til fastgørelsespunktet), hvilket betyder, at dette også kan forårsage et faseskift. Det er derfor atleter bruger blød støtte. Det samme træk er forbundet med anvendelsen af princippet om "ophængt tønde", når våbenets forende ikke har en hård kontakt med tønden og stift er fastgjort til det (våbnet) kun i området omkring modtager, og den anden ende berører enten slet ikke tønden eller rører gennem en fjederbelastet samling (SVD).
Endelig tanke. Det faktum, at det med den samme tøndelængde er umuligt at opnå samme nøjagtighed ved forskellige temperaturer, giver en glimrende grund til at strække hjernen. Det er kun nødvendigt at ændre længden og / eller massen af tønderen, når tøndeens temperatur ændres. Uden at ændre hverken længden eller vægten af tønden. Set fra humaniora er dette et paradoks. Set fra en teknikers synspunkt er det en ideel opgave. Hele en designer liv er forbundet med løsningen af sådanne problemer. Sherlockerne hviler.







